Davis® causal correlation analysis
- Latest Dynatrace
- Explanation
- 9-min read
- Published Nov 02, 2022
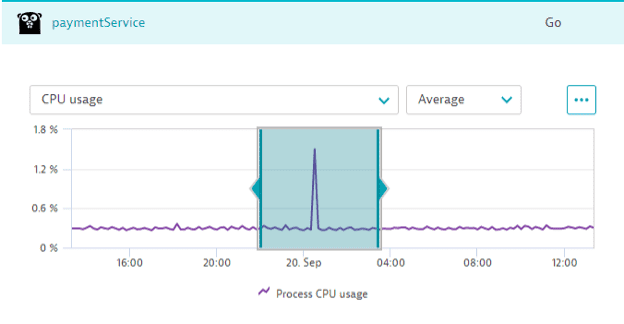
The causal correlation analysis seamlessly combines topological context with metric data to quickly identify observability signals relevant to any signal behavior (for example, a spike on a chart) that you want to investigate. The analysis enables you to quickly find and explore time series with similar behavior to the one you're investigating.
Causal correlation analysis operates with two essential pieces of data:
- Reference time series: the time series you're investigating, along with the selected timeframe, resolution, and scale of the chart where the analysis started. There can only be one reference time series.
- Candidate time series: a set of time series that Davis assembles automatically based on their similarity and relation to the reference time series. To assemble the set, Davis uses the topological and domain context of the reference time series. For example, every metric from a page in the web UI, where you trigger the analysis is automatically included in the candidate set. The candidate set might consist of hundreds or thousands of time series.
Analysis methodology
Davis compares the reference time series to each candidate time series and calculates a Pearson correlation coefficient. Then, based on this coefficient and penalties for applied transformations, signal adoptions, and relevance assessments, the analysis produces a similarity score for each candidate time series. The similarity score has the range from 0.0 (no similarity) to 1.0 (high similarity).
All analysis steps (for example, resolving context-related metric queries, data conversion, and output formatting) are fully automated.
Because every entity-analysis page in the Dynatrace web UI uses configured topology relationships to load entity and context-relevant information, Davis considers this information for the analysis. Every time series shown on a page is included in the candidate set.
For example, if you start the analysis from a host page, the set of candidate time series includes all host metrics, all metrics of disks on the host, all metrics of processes running on the host, and many more.
Signal transformations
To better cope with signal fluctuations, noise, and uncertainties, Davis applies various transformations to candidate time series. Two types of transformation are applied:
- Time shift
- Smoothing
Each transformation applied to a time series produces a penalty to its score. The penalty depends on how much the original signal was transformed: the more the time series is transformed, the higher is the penalty. The output of the analysis never contains multiple variations of the same candidate time series. Only the one with the highest score is included. If multiple variations have the same scores, the one with less penalties is preferred.
Time shift transformation
The time shift transformation aims to cope with signals that are similar in behavior but shifted in time. Possible reasons for such a shift include signal source delays or differences in the measurement cycles used by sensors.
The analysis automatically includes positive and negative shifts of up to 2 resolution steps to the candidates set. The image below illustrates this subset of candidates: an original time series in one-minute resolution plus one- and two-minute shifts in each direction.
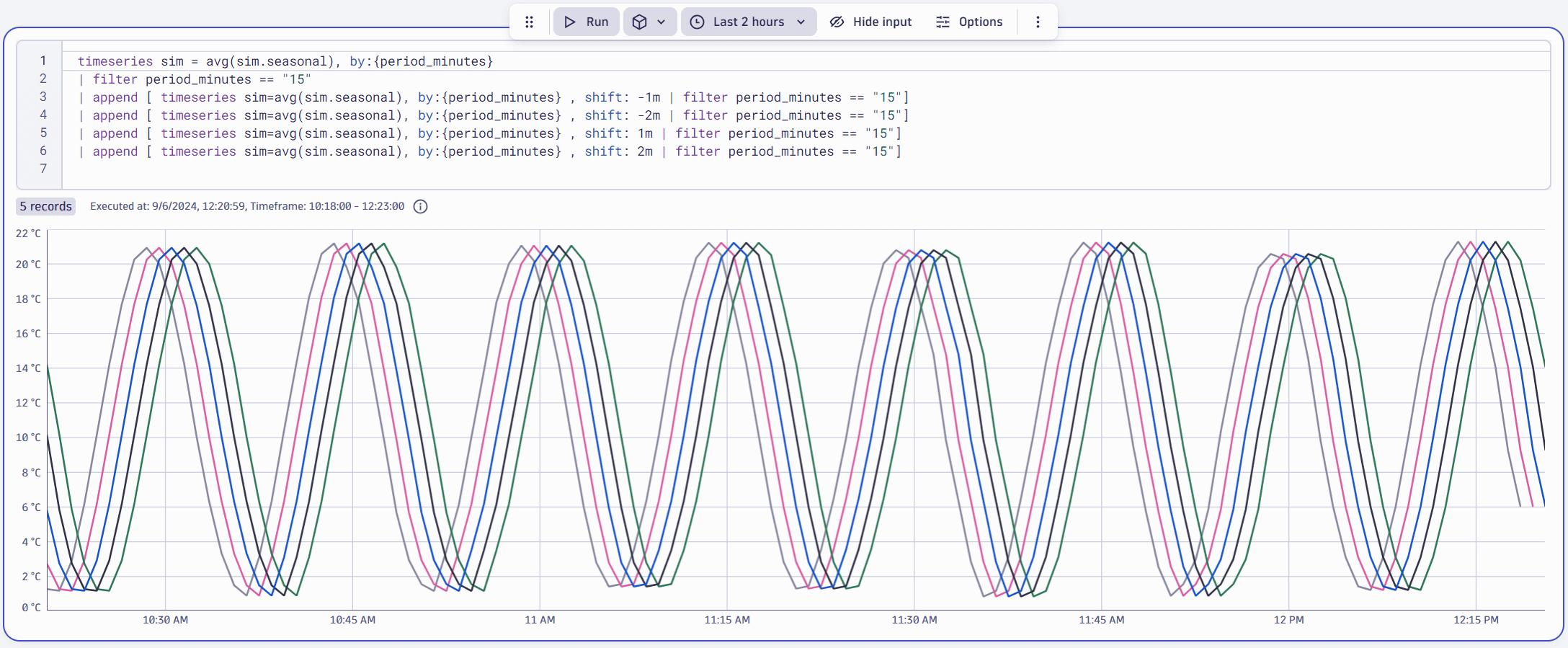
A penalty of 0.004 is deducted from the score per shift in either direction. For example, the time series shifted two steps into the past receives the penalty of 0.008 and the one shifted one step into the future receives the penalty of 0.004.
Show time-shift penalty table
| Time shitf (resolution steps) | Penalty |
|---|---|
| -2 | 0.008 |
| -1 | 0.004 |
| 0 | 0 |
| 1 | 0.004 |
| 2 | 0.008 |
Smoothing transformation
The smoothing transformation aims to distinguish the signal you're interested in from the unwanted noise.
Casual correlation analysis automatically includes smoothing transformations of moving averages of two and three resolution steps to the candidates set. The image below illustrates this subset of candidates: an original time series in one-minute resolution plus two- and three-minute moving averages.
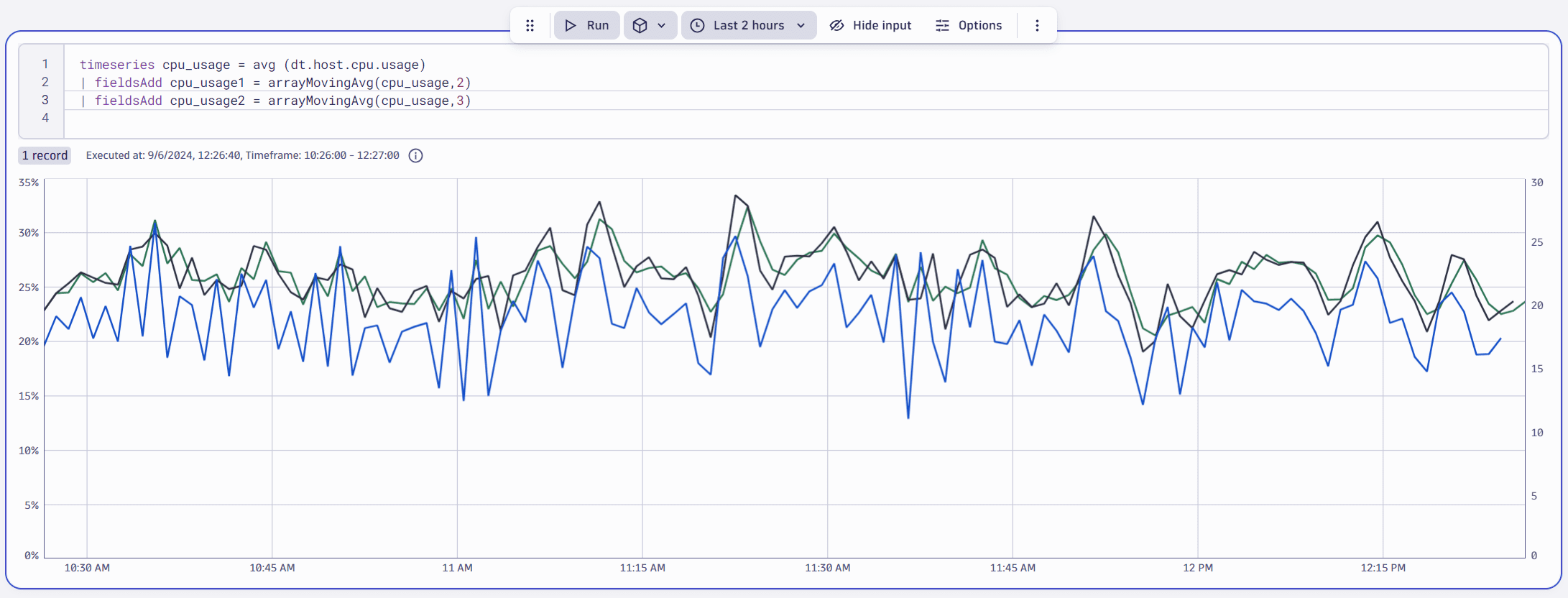
The penalty for the smoothing transformation is calculated using the following formula: 0.01 × (window width − 1).
Show smoothing penalty table
| Window width | Penalty |
|---|---|
| 1 | 0 |
| 2 | 0.01 |
| 3 | 0.02 |
Pearson correlation coefficient
The Pearson correlation coefficient represents the basis for the score calculation. A reference time series is correlated with each candidate time series, including all transformed variants. For example, for a candidate set of 5000 time series and default transformation settings, a total of 150,000 time series correlations are calculated
The coefficient is calculated in a two-pass algorithm. The first pass normalizes each time series (reference and all candidates) by subtracting the mean and dividing by the standard deviation. The second pass calculates the cross-correlation between the normalized reference and each normalized candidate time series.
Time shift handling
A negative shift of X ignores the first X elements of the reference series (as if they were removed) for the cross-correlation, effectively reducing the number of considered values for both time series. Thus, the cross-correlation compares candidates with earlier time stamps to references with later time stamps.
In turn, a positive shift of X ignores the first X elements of the candidate series. Thus, the cross-correlation compares candidates with later time stamps to references with earlier time stamps.
Smoothing handling
For each reference-candidate pair, two smoothed (resampled) time series variations are created by applying a moving mean of the specified window size. Smoothing happens to reference and candidate time series alike, and only pairs with the same smoothing window are correlated (that is, a reference with a smoothing window of 1 and a candidate with a smoothing window of 2 are not considered).
Result ranking
The causal correlation analysis returns a score (based on the Pearson correlation coefficient and transformation penalties) for each candidate that describes the similarity of the candidate in the range from 0.0 (no similarity) to 1.0 (high similarity). The score represents a rank within the results list; it is not a percentage measure. Each resulting time series is visualized along with its score.
While the analyzer identifies positive and negative correlations, Dynatrace does not distinguish them in the visualization, as both are equally relevant for exploratory analysis.
The threshold of 0.75 applies to the results, which means that time series with a lower score are excluded from the result.
| Correlation threshold | 0.0 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.65 | 0.7 | 0.75 | 0.8 | 0.85 | 0.9 | 0.95 |
| Minimum data points | 1001 | 261 | 121 | 66 | 41 | 28 | 23 | 19 | 16 | 14 | 12 | 10 | 8 |
A lower threshold would require more data points to ensure the low (below 0.1%) chance of unrelated time series being included in the result by accident. Since this is less likely for a high threshold, it requires fewer data points, and therefore this threshold was chosen. The minimal amount of data points is calculated using a Student's t-test.
Start exploratory analysis
You can trigger an exploratory analysis from any unified analysis page (for example, a host overview page or a Kubernetes workload page).
-
In the Dynatrace web UI, navigate to the relevant unified analysis page (host overview, service, Kubernetes workload, or other).
-
Select the phenomenon you want to analyze on a chart.
Every data analysis relies on the quality of your data. The quality of the results significantly improves when you select a phenomenon correctly.
Causal correlation analysis requires that portions of normal behavior in a reference time series be selected–both before and after any phenomenon under analysis. For a spike analysis, a rule of thumb is that the spike itself should cover a third of the reference time series, with one third before and one third after the spike.
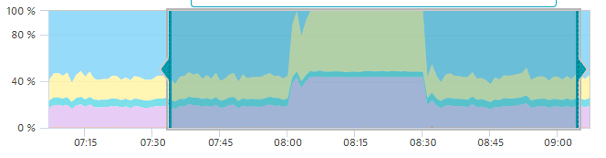
Here's an example of an inaccurate time-series selection: only the plateau is selected, which will result in noisy, unexpected results.
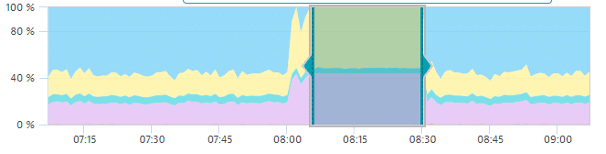
-
Select Analyze and, if needed, the metric for analysis. If the Analyze option is disabled—you didn't select enough data points—expand the selection.
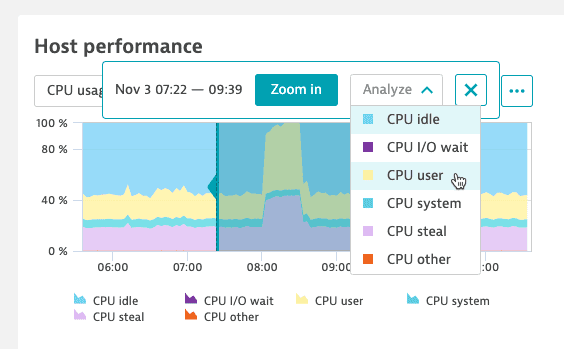
-
Davis gathers the candidate set (all the metrics displayed on the page are included automatically) and starts the analysis. The results are displayed in the side panel on the right. The results are ranked based on their similarity score.
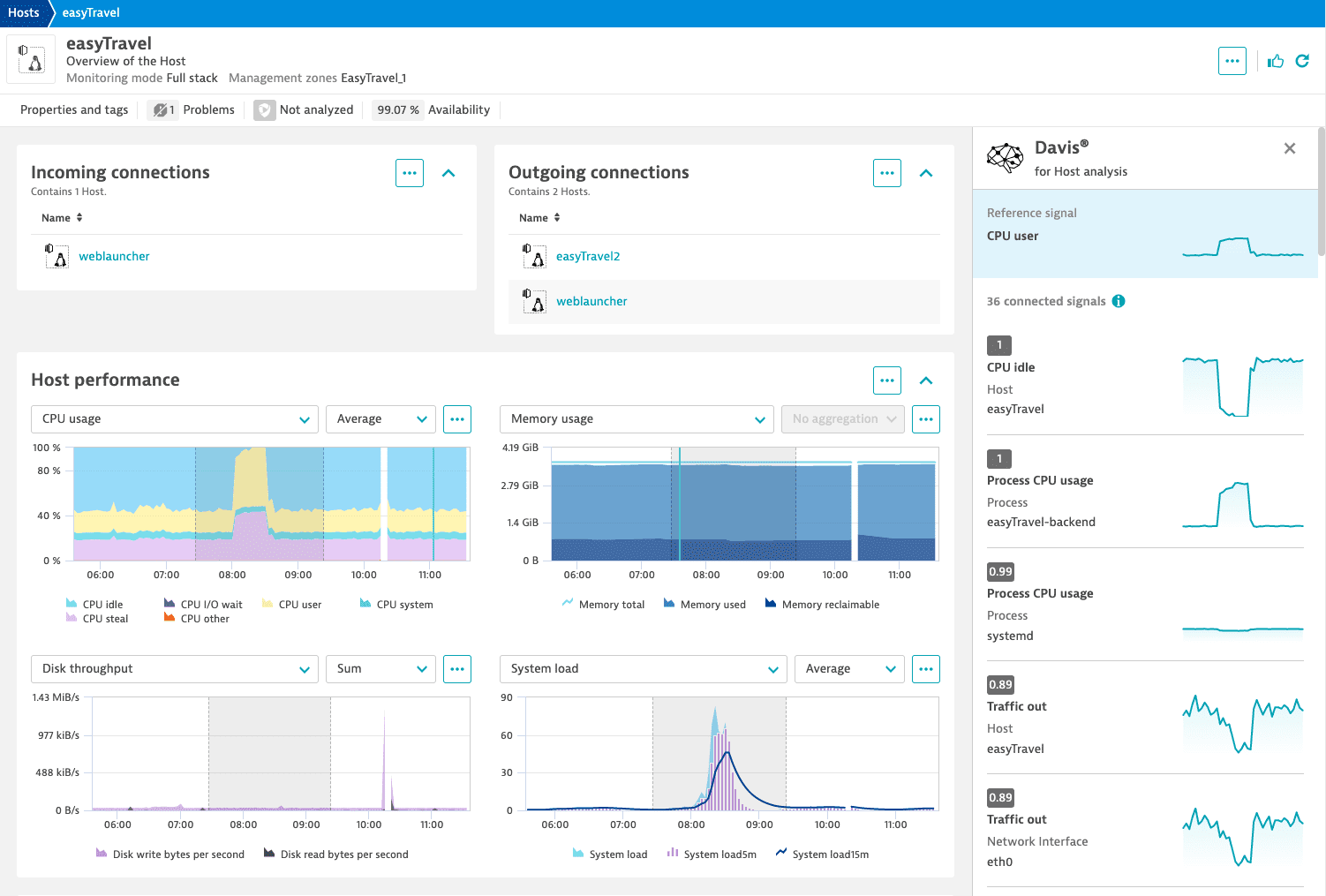
Every chart in the result pane acts as a link to the metric—select it to go to the original chart. Note that the original chart might look slightly different due to different scaling.
Limitations
- A certain number of data points is required for high-quality results. A lack of data points significantly increases the chance of inaccurate results.
- Candidate time series must have enough data points in the selected timeframe. Even if you selected enough data points in the reference time series, candidates might miss the data for the same timeframe.
- Signals must have significant variance. Nearly flat time series will produce spurious correlations (noisy detections).